A Treatise on data and steals

I think I’ve read this about a dozen times by now. I love it for the simple reason that it does exactly what analyzing data is supposed to–allow us to see what we would otherwise be unable or unwilling to see. The author also had the guts to break out some bigger statistical guns and use multiple regressions, a technique I’ve also used before.

As the nerdy stat head data junkie of this blog, I want to take this opportunity to really emphasize the most fundamental premise of data-based analysis. Data is non-partisan. People are not.  When you hear the terms data-driven or data-based decision-making, that means the data comes before the decision, not vice versa. The worst, and unfortunately most common, mistake when working with data is to use data analysis to reinforce an already formed conclusion, or at least a very desired conclusion. In such a scenario, the person who thinks his/her opinion is slighted simply dismisses the results of the data analysis as opposed to rethinks his/her original conclusion.

And that makes sense. If you poured $20 million dollars into a program to improve urban poverty, but the data say your program has not improved anything, it’s hard to simply accept that. It’s much easier to call the data analysis baloney and keep believing that your program is doing well. But we can all see why such a decision would be dangerous and potentially financially calamitous. The same thing goes for basketball. If you refuse to buy into data simply because you disagree with the results, are you doing yourself (or others if you’re in such a position) any favors? Do you have the balls to eschew your pre-formed opinions and allow the data to inform new ones? It’s not easy, but if we can’t or refuse to then there is absolutely no need to do any more data analysis on anything.

Onto steals.

First, because we are good consumers of data and don’t just dismiss analysis because we don’t like the results, we’re going to assume that Benjamin Morris’s results are statistically accurate. Where can we go from here? The two most common “fair game” criticisms of data analysis are the data itself (is it accurate?) and the analysis methods (are they appropriate?). I’m going to assume that the data is accurate. Since he didn’t publish his methods, I can’t comment on them. What I can do is take his brilliant ideas and go in a separate direction with them.

Benjamin wanted to know the impact of individual box scores on team production. I don’t have the patience to grab that much data, so I’m going to look at the impact of team box score stats on team production. Since I’ve already established that I’m impatient, I purposefully sampled box score stats from five teams, the Houston Rockets, Indiana Pacers, Miami Heat, OKC Thunder, and Chicago Bulls. I selected the Rockets because I write for this blog. I selected the other four teams because they’re successful but play very different styles of basketball.

Then I did the exact thing that Benjamin did, but on a team level. I ran a regression using a bunch of box score stats to see how each stat predicted team performance, when all other stats were held equal. I also controlled for strength of opponent. Here are the results.

I broke up team productivity into opponent points (team defense) and team points (team offense). To read this, let’s take rebounds. Each additional team rebound is worth 0.249 additional points for a player’s team, and takes away -0.358 points from the opponent’s team. I didn’t include assists because they automatically result in points, which kind of defeats the purpose of prediction.

As you can see, the results support Benjamin’s findings (love when this happens!). Steals are monstrously valuable and equate to more team points than any other box score stat. Surprisingly, steals don’t predict anything on defense (neither do turnovers). So despite being a defensive statistic, steals are much more valuable offensively. Also surprising, at least to me, is that fouls actually predict more team points. My interpretation is that aggressive play that results in steals probably also results in fouls. So both more fouls and more steals might predict easy fast break points, though fouling is a wash because an extra foul predicts 0.583 extra points for the opponent.

One methodological criticism about the steals analysis I’ve noticed, both on the forums here and on FiveThirtyEight, is that there are fewer steals in a game than, say, rebounds, and therefore it’s not really a fair comparison. While the phrasing isn’t technically correct, the general sentiment of this criticism is. Think of it this way. You want to predict your happiness. Your stats are beers and cars. It won’t surprise you that an extra car makes you a lot happier than an extra beer, but that’s not really fair because you can get another beer a lot more easily than you can get another car. What we need to do is standardize the stats.

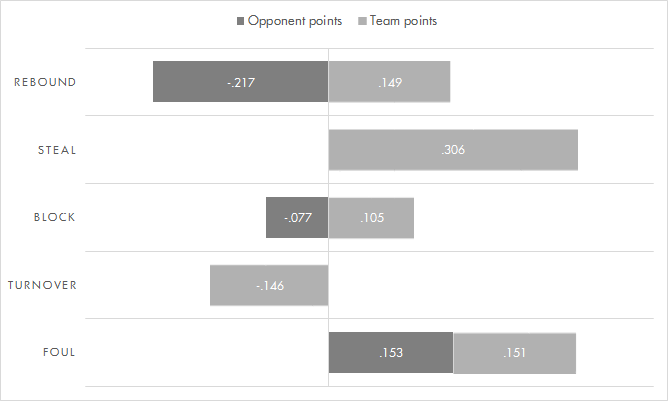
That’s what I did next. Instead of units (e.g., one extra rebound or steal) and points, I converted everything into standard deviations. Here are the results.

The way to read this is as such, using rebounds as an example. An increase in one standard deviation of rebounds predicts a decrease of 0.217 standard deviations of opponent points, and an increase of 0.149 standard deviations of team points. That sounds like gibberish, and it is. What’s valuable about this is that it allows us to compare stats without worrying about the beer/car problem, since standard deviations are equivalently sized units. From these results, we see that steals are still the strongest single predictor of team or opponent points. However, the difference between steals and other categories is smaller. Compared to a rebound, it is only about twice as valuable, as opposed to roughly five times as valuable in the previous chart. Rebounds do have the added benefit of taking away opponent points, so from the perspective of net points a rebound is actually more valuable than a steal.

View this discussion from the forum.